Bayesian Filters¶
This module contains Bayesian filters.
All classes from this module are currently imported to top-level pybayes module, so instead of from pybayes.filters import KalmanFilter you can type from pybayes import KalmanFilter.
Filter prototype¶
- class pybayes.filters.Filter[source]¶
Abstract prototype of a bayesian filter.
- bayes(yt, cond=None)[source]¶
Perform approximate or exact bayes rule.
Parameters: - yt (1D numpy.ndarray) – observation at time t
- cond (1D numpy.ndarray) – condition at time t. Exact meaning is defined by each filter
Returns: always returns True (see posterior() to get posterior density)
- posterior()[source]¶
Return posterior probability density funcion (CPdf).
Returns: posterior density Return type: Pdf Filter implementations may decide to return a reference to their work pdf - it is not safe to modify it in any way, doing so may leave the filter in undefined state.
- evidence_log(yt)[source]¶
Return the logarithm of evidence function (also known as marginal likelihood) evaluated in point yt.
Parameters: yt (numpy.ndarray) – point which to evaluate the evidence in Return type: double This is typically computed after bayes() with the same observation:
>>> filter.bayes(yt) >>> log_likelihood = filter.evidence_log(yt)
Kalman Filter¶
- class pybayes.filters.KalmanFilter(A, B=None, C=None, D=None, Q=None, R=None, state_pdf=None)[source]¶
Implementation of standard Kalman filter. cond in bayes() is interpreted as control (intervention) input
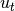 to the system.
to the system.Kalman filter forms optimal Bayesian solution for the following system:
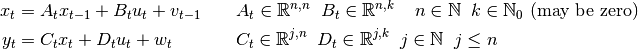
where
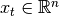 is hidden state vector,
is hidden state vector, 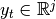 is
observation vector and
is
observation vector and 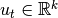 is control vector.
is control vector. 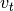 is normally
distributed zero-mean process noise with covariance matrix
is normally
distributed zero-mean process noise with covariance matrix 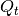 ,
, 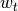 is normally
distributed zero-mean observation noise with covariance matrix
is normally
distributed zero-mean observation noise with covariance matrix 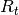 . Additionally, intial
pdf (state_pdf) has to be Gaussian.
. Additionally, intial
pdf (state_pdf) has to be Gaussian.- __init__(A, B=None, C=None, D=None, Q=None, R=None, state_pdf=None)[source]¶
Initialise Kalman filter.
Parameters: - A (2D numpy.ndarray) – process model matrix
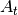 from class description
from class description - B (2D numpy.ndarray) – process control model matrix
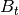 from class description; may be None or unspecified for control-less systems
from class description; may be None or unspecified for control-less systems - C (2D numpy.ndarray) – observation model matrix
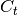 from class description; must be full-ranked
from class description; must be full-ranked - D (2D numpy.ndarray) – observation control model matrix
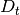 from class description; may be None or unspecified for control-less systems
from class description; may be None or unspecified for control-less systems - Q (2D numpy.ndarray) – process noise covariance matrix
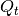 from class description; must be positive definite
from class description; must be positive definite - R (2D numpy.ndarray) – observation noise covariance matrix
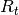 from class description; must be positive definite
from class description; must be positive definite - state_pdf (GaussPdf) – initial state pdf; this object is referenced and used throughout whole life of KalmanFilter, so it is not safe to reuse state pdf for other purposes
All matrices can be time-varying - you can modify or replace all above stated matrices providing that you don’t change their shape and all constraints still hold. On the other hand, you should not modify state_pdf unless you really know what you are doing.
>>> # initialise control-less Kalman filter: >>> kf = pb.KalmanFilter(A=np.array([[1.]]), C=np.array([[1.]]), Q=np.array([[0.7]]), R=np.array([[0.3]]), state_pdf=pb.GaussPdf(...))
- A (2D numpy.ndarray) – process model matrix
- bayes(yt, cond=None)[source]¶
Perform exact bayes rule.
Parameters: - yt (1D numpy.ndarray) – observation at time t
- cond (1D numpy.ndarray) – control (intervention) vector at time t. May be unspecified if the filter is control-less.
Returns: always returns True (see posterior() to get posterior density)
Particle Filter Family¶
- class pybayes.filters.ParticleFilter(n, init_pdf, p_xt_xtp, p_yt_xt, proposal=None)[source]¶
Standard particle filter (or SIR filter, SMC method) implementation with resampling and optional support for proposal density.
Posterior pdf is represented using EmpPdf and takes following form:
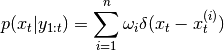
- __init__(n, init_pdf, p_xt_xtp, p_yt_xt, proposal=None)[source]¶
Initialise particle filter.
Parameters: - n (int) – number of particles
- init_pdf (Pdf) – either EmpPdf instance that will be used directly as a posterior (and should already have initial particles sampled) or any other probability density which initial particles are sampled from
- p_xt_xtp (CPdf) –
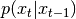 cpdf of state in t given state in t-1
cpdf of state in t given state in t-1 - p_yt_xt (CPdf) –
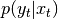 cpdf of observation in t given state in t
cpdf of observation in t given state in t - proposal (Filter) – (optional) a filter whose posterior will be used to sample
particles in bayes() from (and to correct their weights). More specifically,
its bayes
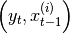 method is called before sampling
i-th particle. Each call to bayes() should therefore reset any effects of
the previous call.
method is called before sampling
i-th particle. Each call to bayes() should therefore reset any effects of
the previous call.
- bayes(yt, cond=None)[source]¶
Perform Bayes rule for new measurement
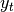 ; cond is ignored.
; cond is ignored.Parameters: cond (numpy.ndarray) – optional condition that is passed to 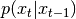 after
after  so that is can be rewritten as:
so that is can be rewritten as: 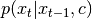 .
.The algorithm is as follows:
- generate new particles:
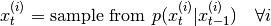
- recompute weights:
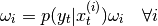
- normalise weights
- resample particles
- generate new particles:
- class pybayes.filters.MarginalizedParticleFilter(n, init_pdf, p_bt_btp, kalman_args, kalman_class=<class 'pybayes.filters.KalmanFilter'>)[source]¶
Simple marginalized particle filter implementation. Assume that tha state vector
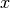 can be divided into two parts
can be divided into two parts 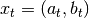 and that the pdf representing the process
model can be factorised as follows:
and that the pdf representing the process
model can be factorised as follows: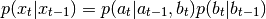
and that the
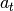 part (given
part (given 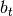 ) can be estimated with (a subbclass of) the
KalmanFilter. Such system may be suitable for the marginalized particle filter, whose
posterior pdf takes the form
) can be estimated with (a subbclass of) the
KalmanFilter. Such system may be suitable for the marginalized particle filter, whose
posterior pdf takes the form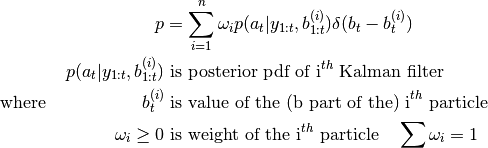
Note: currently
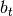 is hard-coded to be process and observation noise covariance of the
is hard-coded to be process and observation noise covariance of the
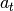 part. This will be changed soon and
part. This will be changed soon and 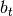 will be passed as condition to
KalmanFilter.bayes().
will be passed as condition to
KalmanFilter.bayes().- __init__(n, init_pdf, p_bt_btp, kalman_args, kalman_class=<class 'pybayes.filters.KalmanFilter'>)[source]¶
Initialise marginalized particle filter.
Parameters: - n (int) – number of particles
- init_pdf (Pdf) – probability density which initial particles are sampled from. (both
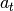 and
and 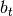 parts)
parts) - p_bt_btp (CPdf) –
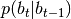 cpdf of the (b part of the) state in t given
state in t-1
cpdf of the (b part of the) state in t given
state in t-1 - kalman_args (dict) – arguments for the Kalman filter, passed as dictionary; state_pdf key should not be speficied as it is supplied by the marginalized particle filter
- kalman_class (class) – class of the filter used for the
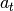 part of the system;
defaults to KalmanFilter
part of the system;
defaults to KalmanFilter
- bayes(yt, cond=None)[source]¶
Perform Bayes rule for new measurement
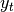 . Uses following algorithm:
. Uses following algorithm:- generate new b parts of particles:
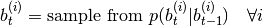
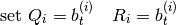 where
where 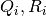 is
covariance of process (respectively observation) noise in ith Kalman filter.
is
covariance of process (respectively observation) noise in ith Kalman filter.- perform Bayes rule for each Kalman filter using passed observation
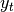
- recompute weights:
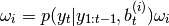 where
where
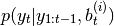 is evidence (marginal likelihood) pdf of ith Kalman
filter.
is evidence (marginal likelihood) pdf of ith Kalman
filter. - normalise weights
- resample particles
- generate new b parts of particles: